Υπολογιστής τυπικής απόκλισης

Enter Inputs	5,20,40,80,100 Enter the Numbers with Comma separated(,)

Result:
No.of Inputs
Mean
Standard Deviation(SD)
Population Standard Deviation(PSD)
Variance(SD)
Variance(PSD)
Calculation

Ο υπολογιστής τυπικής απόκλισης για τον υπολογισμό της κοινής μέτρησης της εξάπλωσης ενός συνόλου δεδομένων, είναι μια ανάλυση δεδομένων. Η αριθμομηχανή θα μπορούσε να σας δώσει αριθμό εισροών, μέσων, τυπικής απόκλισης (SD), τυπική απόκλιση πληθυσμού (PSD), διακύμανση (SD), διακύμανση (PSD) μιας δεδομένης τιμών εισόδου του συνόλου δεδομένων.

Τυπική φόρμουλα απόκλισης

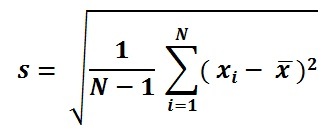
Standard Deviation Formula & Calculation

Πληθυσμός SD Formula

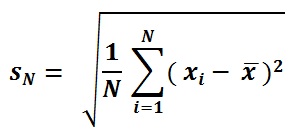
PSD - Population Standard Deviation Formula & Calculation

Τύπος διακύμανσης

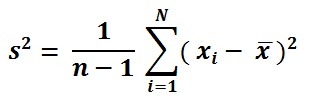
Variance Formula & Calculation

Μέσος τύπος

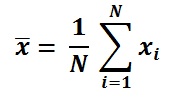
Mean Formula & Calculation

Για παράδειγμα, όταν δίνεται ένα σύνολο δεδομένων 5,20,40,80,100 , το αποτέλεσμα θα είναι:

Συνολικές εισροές (n) = (5,20,40,80,100)

Συνολικές εισόδους (n) = 5

Μέσος όρος (xm) = (x1 + x2 + x3 ... xn) / n

Μέσος όρος (xm) = 245/5

Μέσα (xm) = 49

-------------------------------------------

Sd =

SQRT (1 / (Ν-1) * ((Χ1-ΧΜ) ^ 2 + (Χ2-ΧΜ) ^ 2 +. + (XN-XM) ^ 2))

= SQRT (1 / (5-1) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2 )

= SQRT (1/4 ((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2)))

= SQRT (1/4 (((1936) + (841) + (81) + (961) + (2601)))

= SQRT (1605)

= 40.0625

Διακύμανση = sd ^ 2

Διακύμανση = 40.0625 ^ 2

Διακύμανση = 1605

-------------------------------------------

Psd =

SQRT (1 / (n) * ((x1-xm) ^ 2 + (x2-xm) ^ 2 +. + (xn-xm) ^ 2))

= SQRT (1 / (5) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2))

= SQRT (1/5 ((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2)))

= SQRT (1/5 ((1936) + (841) + (81) + (961) + (2601))))

= SQRT (1284)

= 35.8329

Διακύμανση = sd ^ 2

Διακύμανση = 35.8329 ^ 2

Διακύμανση = 1284

Υπολογιστής τυπικής απόκλισης

FoxCalculators - Δωρεάν υπολογιστές στο διαδίκτυο!