FoxCalculators - Δωρεάν υπολογιστές στο διαδίκτυο!

Ένας ιδιοτιμέας ενός τετραγωνικού μήτρα Α είναι ένας μη μηδενικός φορέας V ότι, όταν η μήτρα πολλαπλασιάζεται με V, αποδίδει ένα σταθερό πολλαπλάσιο του V, ο πολλαπλασιαστήρας που συνήθως δηλώνεται από λ. Δηλαδή: a v = λ '

(Επειδή αυτή η εξίσωση χρησιμοποιεί μετα-πολλαπλασιασμό από το V, περιγράφει ένα σωστό ιδιοτιμή.) Ο αριθμός λ ονομάζεται Eigenvalue ενός αντίστοιχου σε v.

Όλες οι ιδιοτιμές και οι ιδιοτιμώνες ικανοποιούν την εξίσωση AX = ΛΧ για ένα δεδομένο τετράγωνο μήτρα Α.

Απλός υπολογιστής μήτρας για τον υπολογισμό της τιμής EIGEN και τον EIGEN φορέα μιας μήτρας 3x3. Καταχωρίστε τις τιμές της Matrix 3x3 και κάντε κλικ στο κουμπί Υπολογίστε.

Ιχνος

Το ίχνος, το TR (Α) ενός τετραγωνικού μήτρα Α είναι το άθροισμα των διαγώνων καταχωρήσεών του. Ενώ ο πολλαπλασιασμός του Matrix δεν μετακρίνεται όπως αναφέρθηκε παραπάνω, το ίχνος του προϊόντος δύο μήτρων είναι ανεξάρτητο από τη σειρά των παραγόντων:

tr (ab) = tr (ba).

Αυτό είναι άμεσο από τον ορισμό του πολλαπλασιασμού του Matrix:

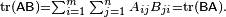
Επίσης, το ίχνος μιας μήτρας είναι ίσο με αυτό της μεταφοράς, δηλ.,

tr (a) = tr (a ^{t ).}