Τραπεζοειδείς αριθμομηχανή με γωνίες

Parallel Side a:  
Parallel Side b:  
Angle (θ):
Angle (Φ)
Altitude (h):  
 
Area:  
Perimeter:  
Side c:  
Side d:  
Diagonal L1H2:  
Diagonal H1L2:  

Στην ευκλείδικη γεωμετρία, ένα τραπεζοειδές έχει δύο παράλληλες πλευρές ονομάζονται βάσεις του τραπεζοειδούς. Οι άλλες δύο πλευρές καλούν τις πλευρικές πλευρές.

Τραπεζοειδείς τύποι

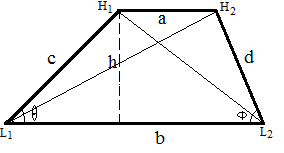
1. Περιοχή = Η (Α + Β) / 2

2. Perimeter = a + b + c + d

3. Διαγώνιο L 1 h 2 = SQRT (H 2 + (B-SQRT (C 2 2 )) 2 )

4. Διαγώνια H 1 l 2 = SQRT (H 2 + (B 2 2 )) 2 )

Για παράδειγμα, όταν παράλληλη πλευρά Α = 3, Β = 4, γωνία (θ) = 0,9273, γωνία (φ) = 0,6082, υψόμετρο (Η) = 4, στη συνέχεια η περιοχή = 14, περίμετρος = 19, πλευρά C = 5, πλευρά d = 7, διαγώνιο L1H2 = 4.1231, διαγώνιο H1L2 = 4.3641.

Τραπεζοειδείς αριθμομηχανή με γωνίες
Αριθμομηχανές προτάσεων Resolver desigualdades lineares Calculadora de distribuição hipergeométrica Calculadora de equação sexta Calculadora científica online. Efeito da calculadora de tamanho Equações de Transposição Resolvendo a calculadora Sinal para a calculadora de relação de ruído Calculadora do produto Cruz do vetor Calculadora de adição de vetor Calculadora de convolução online. Soma de calculadora consecutiva cubos Soma de calculadora de praças Soma de calculadora de quadrados consecutivos Calculadora de conjuntos de diferença simétrica Calculadora de teorema binômio