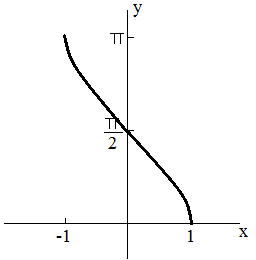Αριθμομηχανή αρκοκοσίνης

arccos

Στα μαθηματικά, οι αντίστροφες τριγωνομετρικές λειτουργίες είναι οι αντίστροφες λειτουργίες των τριγωνομετρικών λειτουργιών.

arccos 0,5 = cos-1 0,5 = 60º 0 '0 "= 60º + K × 360º (k = ..- 1,0,1, ...) = -300º, 60º, 420º, .. = 1.04719755rad + k × 2π (k = ..- 1,0,1, .. = -1.66666667Π, 0.33333333Π, 2.33333333π, ..

arccos -0.3 = cos-1 -0,3 = 107º 27 '27.371 "= 107.45760312º + K × 360º (k = ..-1,1, ..) = -252.54239688º, 107.45760312º, 467.45760312º, 467.45760312º, 467.45760312º, = 1.87548898rad + k × 2π (k = ..- 1,0,1, .. = -1.40301332Π, 0.59698668Π, 2.59698668Π, ..

y = arccos (x) γράφημα

y

(Βαθμούς)

y

(Radian)

x

180 ̊

π

- 1

150 ̊

5π / 6

- 0.866025

135 ̊

3Π / 4

- 0.707107

120 ̊

2Π / 3

- 0.5

90 ̊

π / 2

0

60 ̊ π / 3

0.5

45 ̊

π / 4

0.707107

30 ̊

π / 6

0.866025

0 ̊

0

1

όνομα

συνήθης σημείωση

ορισμός

domain of x για πραγματικό αποτέλεσμα

εύρος συνήθους κύριου αξίας

(ακτίνια)

εύρος συνήθους κύριου αξίας

(βαθμούς)

arcsine

y = arcsin x

x = sin y

-1 ≤ x ≤ 1

-π / 2 ≤ y ≤ o

-90 ° ≤ y ≤ 90 °

arcosine

y = arccos x

x = cos y

-1 ≤ x ≤ 1

0 ≤ y ≤ π

0 ° ≤ y ≤ 180 °

arctangent

y = arctan x

x = tan y

Όλοι οι πραγματικοί αριθμοί

-Π / 2 <<> Y <Π / 2

-90 ° < y <90 °

arccotangent

y = arccot ​​ x

x = cot y

Όλοι οι πραγματικοί αριθμοί

0 << i> y <π 0 ° < y <180 °

arcsecant

y = arcsec x

x = sec y

x ≤ -1 ή 1 ≤ x

0 ≤ y <Π / 2 ή π / 2 < y ≤ π

0 ° ≤ y <90 ° ή 90 ° < y ≤ 180 ° ≤ 180 °

arcosecant

y = arccsc x

x = csc y

x ≤ -1 ή 1 ≤ x

-π / 2 ≤ y <0 ή 0 <<> y ≤ p / 2

-90 ° ≤ y <0 ° ή 0 ° < y ≤ 90 °

Αριθμομηχανή αρκοκοσίνης
Αριθμομηχανές προτάσεων Resolver desigualdades lineares Calculadora de distribuição hipergeométrica Calculadora de equação sexta Calculadora científica online. Efeito da calculadora de tamanho Equações de Transposição Resolvendo a calculadora Sinal para a calculadora de relação de ruído Calculadora do produto Cruz do vetor Calculadora de adição de vetor Calculadora de convolução online. Soma de calculadora consecutiva cubos Soma de calculadora de praças Soma de calculadora de quadrados consecutivos Calculadora de conjuntos de diferença simétrica Calculadora de teorema binômio