Equação cartesiana de uma calculadora de avião

Point A , ,
Point B , ,
Point C , ,
   
Equation of the plane
(given three points)		 x+y+z+=0

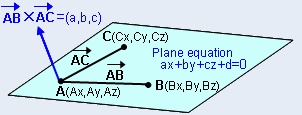
Existem três pontos A (X 1 , Y 1 , Z 1 ), B (X 2 , Y 2 , Z 2 ) e C (x 3 , Y 3 , Z 3 ) deitado em um avião, então a equação de avião pode ser encontrada usando a seguinte fórmula

.

.

.

x - x 1

y - y 1

z - z 1

= 0

X 2 - X 1

y 2 - y 1

Z 2 - Z 1

X 3 - X 1

y 3 - y 1

Z 3 - Z 1

Ou A (AX, AY, AZ), B (BX, BY, BZ), C (CX, CY, CZ), a equação do avião é AX + por + CZ + D = 0

Onde,

a = (By-AY) (CZ-AZ) - (CY-AY) (BZ-AZ)

B = (BZ-AZ) (CX-AX) - (CZ-AZ) (BX-AX)

c = (BX-AX) (CY-AY) - (CX-AX) (BY-AY)

D = - (Aax + Bay + CAZ).

Cálculo da equação de avião cartesiana com as três coordenadas é facilitada aqui.

Equação cartesiana de uma calculadora de avião
Αριθμομηχανές προτάσεων Resolver desigualdades lineares Calculadora de distribuição hipergeométrica Calculadora de equação sexta Calculadora científica online. Efeito da calculadora de tamanho Equações de Transposição Resolvendo a calculadora Sinal para a calculadora de relação de ruído Calculadora do produto Cruz do vetor Calculadora de adição de vetor Calculadora de convolução online. Soma de calculadora consecutiva cubos Soma de calculadora de praças Soma de calculadora de quadrados consecutivos Calculadora de conjuntos de diferença simétrica Calculadora de teorema binômio